So now, I want to talk about light. And more specifically, about electricity, magnetism and how they come together. And I will be honest, I will gloss over a lot of detail, because this is a series on special relativity not electromagnetism, so I won't go in detail. But here are the things you may need to know:
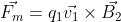
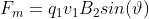 , where the θ represents an angle between the vectors velocity and magnetic field. If they are parallel to each other, then the angle between the two vectors is zero, which means sin(θ) and by extension, F, is null. But if they are perpendicular, then θ is equal to π/2 which means sin(θ) is equal to 1, and:
, where the θ represents an angle between the vectors velocity and magnetic field. If they are parallel to each other, then the angle between the two vectors is zero, which means sin(θ) and by extension, F, is null. But if they are perpendicular, then θ is equal to π/2 which means sin(θ) is equal to 1, and:
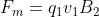 , its maximum value. And if you look, the direction where the force points is always perpendicular to the motion of the body, which means that this force changes the direction of motion.
, its maximum value. And if you look, the direction where the force points is always perpendicular to the motion of the body, which means that this force changes the direction of motion.
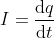
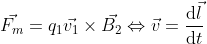
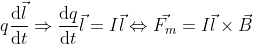
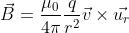
- High school mathematics, specially derivatives
- And hopefully, some pre-calculus, like integrals and such. I would recommend you watch 3blue1brown's series on calculus, because it gives you an intuitive understanding of what a derivative or integral means.
I will use mathematical expressions to summarize the ideas, but I will make an effort to give a written explanation of what they mean, after all, my point for you right now is not for you to understand the math behind it, but to understand that maths give sense to physical conclusions, no matter how unconventional they may seem.
Also, a couple of considerations here. To avoid complexity, I will consider mostly point-like bodies when talking about these equations, because let's be honest, I don't really want to put that much detail into things.
Also, a couple of considerations here. To avoid complexity, I will consider mostly point-like bodies when talking about these equations, because let's be honest, I don't really want to put that much detail into things.
So, the first thing we will talk about today is about Coulomb’s Law, a law that describes the interaction between charged bodies:
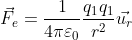
Now, let me give a quick explanation of what does this expression mean. First, let’s explain the constants, you have your classic π, and then you have this symbol ε_0, which in physics is called electric permittivity of the vacuum. It is a physical constant that expresses how vacuum permits electric fields. Now this permittivity may seem a complicated concept, but it essentially says if a certain space is resistant to electric fields (similar to the concept of electric resistance in an electric circuit) and in this particular case, the vacuum permittivity is a constant (at least, we think it is, but is a whole new discussion), it has a specific value, of about 8.854∙10^(-12) m^(-3) kg^(-1) s^4 A^2 (with A being ampere, the unit of current). And four is a number, so we usually just consider all constants assembled in a single constant:
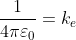
, which we call Coulomb’s constant, and which value is 8.99∙10^9 Nm^2 C^(-2). We can simplify the expression as:
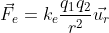
Now, the q_i ,i=1,2, are the charges of the bodies, as of now you can think of them as a fundamental property of matter like mass. And r is the classic distance. So what this expression says is: If you have two bodies with electric charge, they will exert a force on each other that decreases with the square of the distance. Let’s consider their initial distance is A, and they feel a certain force F. If they are at twice the distance A, the force is four times weaker. If they are at half the distance, the force is now 4 times stronger. As for the arrows, as you now, the force is a vector, so it has a direction. And that’s what the last term represent, it shows that for two bodies 1 and 2, the force goes from 1 to 2, and vice-versa. Now if you pay attention, you will see that the formula we have above is like Newton’s Gravitational law:
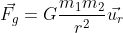
, that describes the interaction between massive bodies. And this is a good way for you to notice a couple of properties for the Coulomb’s force:
First, the intensity of the force does not depend on the direction, but only on distance. Which means it doesn’t matter if you are in any specific point in space, if you are at the same distance, you feel the same strength. That is what we call radial symmetry, and it is something that the gravitational force also presents. Also, you may realize something in the equation, that Newton’s law has a negative sign. Here is something we know in physics (it is more of a convention actually), when forces have negative signs it means they are attractive, while when forces have positive signs they are repulsive. Now, as of right now, we have never found anything with negative mass, so we can be sure Newton’s law is always attractive, but we can’t say the same for Coulomb’s law. We do now there are positive and negative charges, and that means the electrostatic force can be negative and positive depending on the charges, more specifically on the product q_1 q_2. If it is positive (if both charges are positive, or both charges are negative) then the force is repulsive, and they push each other apart. If it’s negative, they have opposite charges, and attract each other.
And that pretty much describes all of the fundamental interactions between charged particles. By the way, the gravitational constant G has a value of like 6.6⋅10^(-11) Nm^2 kg^(-2) which means that Coulomb’s force is like 10^20 times stronger than gravitational force. That's 1 with twenty zeros behind it. Which is why we don’t perceive gravitational force in small scales, like the ones we experience daily, and why all our molecules are bound to each through electrostatic interactions.
Also, I would like to point out about electric fields. As you see from the expression above, force can be described as an interaction between two charged bodies. But it can also be described as an interaction between a charged body and the electric field of another body. This description is particularly useful if our body has some weird shape and consequent charge distribution. We don’t really want to deal with complex integrals that much, but only when necessary. So we can define the force as:
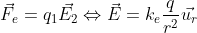
This expression is especially good if you know what is the value of the field, but don’t know where it is coming from, or if you don’t know the source. By the way, you can also describe Newton’s gravitational law as a field equation, like this:
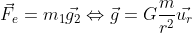
which also has units of acceleration in this case. For Earth’s surface, our gravitational field is approximately 9.8 N/kg or 9.8 m/s^2, the unit of acceleration. So, you can see how useful it is for us to use fields instead. And this is useful if we want to go to the next section. If you want to describe the acceleration caused by an electrostatic force, it would be:
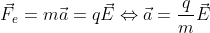
Which means the body would feel an acceleration in the same direction of the electric field. By convention, this is how we show the electric field lines of a charged particle.
Now, let me give a quick explanation of what does this expression mean. First, let’s explain the constants, you have your classic π, and then you have this symbol ε_0, which in physics is called electric permittivity of the vacuum. It is a physical constant that expresses how vacuum permits electric fields. Now this permittivity may seem a complicated concept, but it essentially says if a certain space is resistant to electric fields (similar to the concept of electric resistance in an electric circuit) and in this particular case, the vacuum permittivity is a constant (at least, we think it is, but is a whole new discussion), it has a specific value, of about 8.854∙10^(-12) m^(-3) kg^(-1) s^4 A^2 (with A being ampere, the unit of current). And four is a number, so we usually just consider all constants assembled in a single constant:
, which we call Coulomb’s constant, and which value is 8.99∙10^9 Nm^2 C^(-2). We can simplify the expression as:
Now, the q_i ,i=1,2, are the charges of the bodies, as of now you can think of them as a fundamental property of matter like mass. And r is the classic distance. So what this expression says is: If you have two bodies with electric charge, they will exert a force on each other that decreases with the square of the distance. Let’s consider their initial distance is A, and they feel a certain force F. If they are at twice the distance A, the force is four times weaker. If they are at half the distance, the force is now 4 times stronger. As for the arrows, as you now, the force is a vector, so it has a direction. And that’s what the last term represent, it shows that for two bodies 1 and 2, the force goes from 1 to 2, and vice-versa. Now if you pay attention, you will see that the formula we have above is like Newton’s Gravitational law:
, that describes the interaction between massive bodies. And this is a good way for you to notice a couple of properties for the Coulomb’s force:
First, the intensity of the force does not depend on the direction, but only on distance. Which means it doesn’t matter if you are in any specific point in space, if you are at the same distance, you feel the same strength. That is what we call radial symmetry, and it is something that the gravitational force also presents. Also, you may realize something in the equation, that Newton’s law has a negative sign. Here is something we know in physics (it is more of a convention actually), when forces have negative signs it means they are attractive, while when forces have positive signs they are repulsive. Now, as of right now, we have never found anything with negative mass, so we can be sure Newton’s law is always attractive, but we can’t say the same for Coulomb’s law. We do now there are positive and negative charges, and that means the electrostatic force can be negative and positive depending on the charges, more specifically on the product q_1 q_2. If it is positive (if both charges are positive, or both charges are negative) then the force is repulsive, and they push each other apart. If it’s negative, they have opposite charges, and attract each other.
And that pretty much describes all of the fundamental interactions between charged particles. By the way, the gravitational constant G has a value of like 6.6⋅10^(-11) Nm^2 kg^(-2) which means that Coulomb’s force is like 10^20 times stronger than gravitational force. That's 1 with twenty zeros behind it. Which is why we don’t perceive gravitational force in small scales, like the ones we experience daily, and why all our molecules are bound to each through electrostatic interactions.
Also, I would like to point out about electric fields. As you see from the expression above, force can be described as an interaction between two charged bodies. But it can also be described as an interaction between a charged body and the electric field of another body. This description is particularly useful if our body has some weird shape and consequent charge distribution. We don’t really want to deal with complex integrals that much, but only when necessary. So we can define the force as:
This expression is especially good if you know what is the value of the field, but don’t know where it is coming from, or if you don’t know the source. By the way, you can also describe Newton’s gravitational law as a field equation, like this:
which also has units of acceleration in this case. For Earth’s surface, our gravitational field is approximately 9.8 N/kg or 9.8 m/s^2, the unit of acceleration. So, you can see how useful it is for us to use fields instead. And this is useful if we want to go to the next section. If you want to describe the acceleration caused by an electrostatic force, it would be:
Which means the body would feel an acceleration in the same direction of the electric field. By convention, this is how we show the electric field lines of a charged particle.
Now that you know about electrostatic forces and electric fields, you know one of the main things in electromagnetism. The other thing you need to know is about magnetism. Now the existence of magnetism was known for a long time, ever since Ancient Greece. In Ancient China, compasses were already used as a reliable mode of orientation. And yet it lacked a way for us to properly describe it. No one knew why certain things would attract metals, or why the compasses would always point to the north. The first expression to describe the magnetic field’s behavior has this one:
Now, we have a couple of different things displayed on this expression. First, now we have the velocity appeared, as v, which means the body 1 is moving, and we have this new thing, B. That B is the magnetic field. A current as we know is a collection of moving charges so, what this expression is saying is that a moving charge inside of a magnetic field feels a force that is proportional to both how fast it is moving, and to the strength of the magnetic field it crosses. Now as you see there is a cross product between the two quantities. I hope you already know what a cross-product is but the short explanation I can give is that if you have two vectors and you make a cross-product of them, what you get is another vector perpendicular to both. What this means is that force vector is perpendicular to both the direction of the magnetic field and of the velocity of the particle. Visually, it would probably be something like this.
Now, to be truthful, if it was a negative charge it would be pointing in the opposite way, but this is just for you to visualize what a cross-product mean. Which brings me to another point I want to make that the cross-product as its maximum value if v is perpendicular to B, and its minimum value if v is parallel to be. For you to understand this more intuitively, there is the formula for the absolute value of the force:
Remember when I told you about current? Well, let me just explain it real quick. Current is formally defined as being the variation of charge over time, or:
Which means, in some cases, charge can change over time. So in our previous expression:
If instead of you having a constant charge moving a certain displacement l, you had a certain constant path l where charge would change over time (example: a wire), you could write the expression above as:
You could say that expression describes the strength of a magnetic field on a conducting wire, also called Laplace force.
But there is still a mystery left. Where does the B come from? We know that the electric field E comes from a body with a charge q, but we don’t know the source for B yet. As it turns out, there is an answer for that. Two French physicists, Jean-Baptiste Biot and Felix Savart, where the ones to find a first answer to this question, in a law we now call Biot-Savart Law:
Like with the time we were analyzing Coulomb’s equation, let’s break this one down a bit. First, let’s see which one of these are constants: we have our usual 4 and π, and this time, instead of ε_0, we have µ_0, which is called the magnetic permeability (not permittivity) of the vacuum. It is kind of like permittivity, but instead of determining how resistant (or permissive) is a space to electric fields, it determines how permeable is a space to magnetic fields. And you also have that common factor q/r^2 which means the fields is proportional to the charge that is generating it, and to the distance from that source, like the electric field expression. But the main difference here is on that last term. On the electric field expression, we only had the vector direction u_r that meant the field had radial symmetry over the source. But here we have a cross product between the vector v and the unit direction vector. If you have a cross-product between them can only mean that the field generated is perpendicular to the velocity vector and to the direction. It would look something like this:
If it was a positive particle, the magnetic field would be pointing in the opposite direction.
So while it still holds the radial symmetry of the electric field, the magnetic field has some really interesting characteristics of its own. Like, it is generated by a moving charge, which means that in a place where charges aren’t moving you will not find magnetic fields (not exactly true, but not exactly false either, I just don’t wanna explain more). Now this is most you need to know before we talk about Maxwell and you will finally understand why maybe Galilean Relativity was not the best relativity.
Damn it, this was way longer than I expected. But this is what happens when you try to study half a semester worth of Electromagnetism in one day. Luckily this is not my first encounter with it, and honestly I think it is really important for me to talk about this basic concepts in EM, because we will soon talk about Special Relativity, and then the birth of quantum mechanics. I understand many wouldn't feel comfortable with this much content at once, but you don't have to take it at once. This is not a test, so you don't to be very attentive and fast on learning. But it is important for you to learn if you want to understand anything that may come behind this. Anyway, thank you for your time in here and remember to comment or send me an email at this adress rafaelhoppfer97@gmail.com, for critic or any suggestions you may have.
Some references for you to learn more about this:
- Physics for Students and Engineers (with Modern Physics), Serway & Jewett: Part 4: Electricity and Magnetism, Chapters 23 (23.4-7), 29 (29.1-3), 30(30.1)
For a little more advanced description, we also have this:
- Electromagnetic Fields and Waves, Lorrain & Corson: Chapter 3: Electric Fields(3.1-3)
Chapter 18: Magnetic Fields (18.2)
Also, Wikipedia may give a good introduction on the topic. These books also happen to have a bunch a exercises you can use to pratice, so I highly recommend you to try and solve them, and email me your answers to certain problems, if you are having difficulties.
- Physics for Students and Engineers (with Modern Physics), Serway & Jewett: Part 4: Electricity and Magnetism, Chapters 23 (23.4-7), 29 (29.1-3), 30(30.1)
For a little more advanced description, we also have this:
- Electromagnetic Fields and Waves, Lorrain & Corson: Chapter 3: Electric Fields(3.1-3)
Chapter 18: Magnetic Fields (18.2)
Also, Wikipedia may give a good introduction on the topic. These books also happen to have a bunch a exercises you can use to pratice, so I highly recommend you to try and solve them, and email me your answers to certain problems, if you are having difficulties.





